Numerische Ermittlung von statischen Grenzzuständen und Traglasten bei geomechanischen Problemstellungen
Inhalt
Forschung
Forschung
"Um etwas zu finden musst Du erst einmal suchen",
sagte Thorin immer zu den jugendlichen Zwergen.
"Du findest ganz sicher etwas, wenn Du nur suchst,
allerdings nicht immer das, was Du gesucht hat."
J.R.R. Tolkien, Der Hbbit
Der Mensch muss bei dem Glauben verharren,
dass das Unbegreifliche begreiflich sei;
er würde sonst nicht forschen.
Johann Wolfgang von Goethe
Ich war von September 1997 bis März 2001 wissenschaftlicher Angestellter am Lehrstuhl für Statik der Technischen Universität München und bearbeitete ein Forschungsprojekt der Deutschen Forschungsgemeinschaft (DFG).
Ziel des Projekts
Das Ziel des Projekts bestand in der Entwicklung eines robusten und verlässlichen Finite-Element-Programmes zur numerischen Analyse von Grenzzuständen in der Geomechanik. Neben trockenen, granularen Böden sollten auch wassergesättigte, bindige Böden in die Betrachtungen einbezogen werden. Wesentliche Teilziele waren somit:
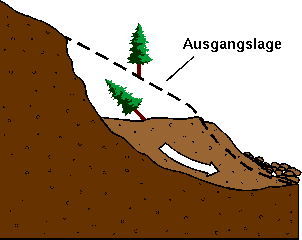
schematische Hanginstabilität
ausgedehnte Hanginstabilität in La Conchita 1995
linienförmige Rutschung in der Nähe von Los Angeles 1998
Lokalisierungsphänomene
Nahezu alle Versagensformen in der Geomechanik sind gekennzeichnet durch Lokalisierungsphänomene. Im Traglastniveau kommt es dabei zu einer starken Konzentration von plastischen Dehnungen in engen Bändern. Bei der numerischen Berechnung mit der Finite-Element-Methode unter Verwendung der klassischen Kontinuumsbeschreibung geht nach einsetzender Scherbandformation die Elliptizität der grundlegenden Differenzialgleichungen verloren. Dies äußert sich in einer Abhängigkeit der Lösung von der verwendeten Maschenweite des FE-Netzes.
Regularisierung
First of all the Ptolemaic system is exploded.
For who will believe that there are as many theories for the Sun as there are planets.
It seems that a single theory of the Sun is enough.
Kepler
Um Lokalisierungsphänomene auch quantitativ geeignet zu beschreiben, müssen Regularisierungsmethoden eingesetzt werden. Im Rahmen des Projektes kamen erweiterte Kontinuumsformulierungen zum Einsatz, mit denen eine Abhängigkeit der FE-Lösung von der Diskretisierungsfeinheit (Maschenweite) vermieden werden konnte:
Beide Methoden beinhalten eine interne Längeneinheit, die für die Breite des auftretenden Scherbandes bestimmend wird. Im ersten Fall wird ein Cosserat-Rotationsfeld eingefürt und durch ein zusätzliches Stoffgesetz an einen Momentenspannungstensor geknüpft. In dieser Beziehung tritt eine interne Länge als Regularisierungsparameter auf. Im zweiten Fall wird Boden als zwei-komponentiges Medium -bestehend aus Korngerüst und Porenfluid- behandelt und Porenwasserdrücke in die Formulierung einbezogen. Auch eine Kopplung der Methoden erscheint in einigen Fällen sinnvoll.
Finite-Element-Methode (FEM)
It is necessary to solve differential equations.
Newton
Da bei wassergesättigten Böden eine Zeitabhängigkeit in die Berechnung eingetragen wird, ist neben der üblichen räumlichen Diskretisierung mit Hilfe der FEM auch der Zeitbereich zu diskretisieren. Als besonders geeignet hat sich hier das Time-Discontinuous-Galerkin-Verfahren herausgestellt. Im Vergleich mit dem oft verwendeten Crank-Nicolson-Schema zeigt es eine höhere Genauigkeit (3. Ordnung) sowie bessere Stabilitätseigenschaften (L-stabil). Darüber hinaus können die auftretenden Sprunggrößen als Fehlerindikatoren im Zeitbereich eingesetzt werden. Als Approximationsgüten wurden verwendet:
Orts- und zeitadaptive Methoden
Already the early finite element man of the 1960's
apparently used intuitive feed back adaptive methods
based on mesh - solve - look - mesh - solve - look.
Schwedische Nationale Enzyklopädie
Um Lokalisierungszonen im räumlichen Bereich genügend fein aufzulösen und gleichzeitig effektive Rechenzeiten zu erhalten waren ortsadaptive Berechnungsmethoden unerlässlich. Mit einem zyklischen Prozess von Berechnung - Fehlerschätzung - Netzanpassung wurde versucht eine Gleichverteilung des Diskretisierungsfehlers über alle Elemente zu erreichen. Zur Berechnung von Fehlermaßen wurden Indikatoren verwendet für den
Als Netzveränderungsstrategie kam die hierarchische Netzverfeinerung zum Einsatz. Eine höhere Netzdichte wurde dabei mit einer Vierteilung von Elementen mit hohem Fehlermaß erreicht.
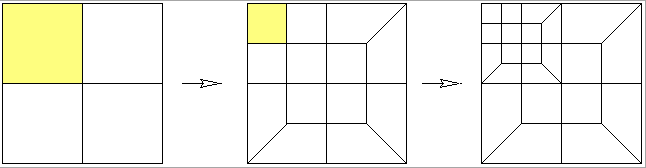
Eine automatische Zeitschrittsteuerung stützt sich auf die Kontrolle des
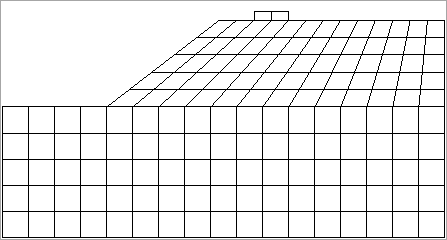
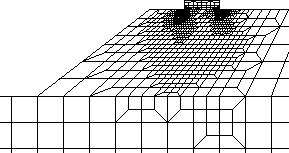
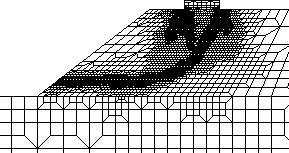
Berechnungsbeispiele
Als numerische Beispiele wurde eine Böschungsinstabilität und ein Grundbruch simuliert. Die Ergebnisse zeigen, dass die FE-Analyse durchaus in der Lage ist, reelle Grenzzustände zu ermitteln. Dementsprechend ergeben sich bei der Böschung ein Gleitkreis und beim Grundbruch eine, dem Gleitlinienfeld nach Prandtl ähnliche Versagensform.
Simulation eines Biaxialversuchs (Filmdarstellung)
Ein typisches Testbeispiel zur Simulation von Materialinstabilitäten stellt der Biaxialversuch dar. Das statische System zeigt die folgende Abbildung
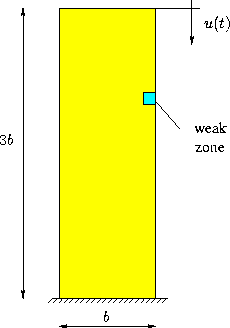
Durch die Schwächung wird ein diagonal durch die Probe verlaufendes Scherband erzeugt, das für das unsymmetrische Schubversagen verantwortlich ist. Ein kleiner Film zeigt, was dabei in der Probe passiert.
zum Seitenanfang